Illumination and Shading in Computer Graphics

Illumination Models:

An illumination Model is a formula in variables associated with the surface properties and light conditions to calculate the intensity of light reflected from a point on a surface.
1. Ambient Light
2. Diffused Light
3. Specular Reflected Light

Ambient Light:

An object may be visible even if it is not directly exposed to a light source. That is because some light is always scattered from the nearby illuminated objects and surroundings. This is called Ambient light. This light is diffused and non-directional and it is assumed to be incident with uniform intensity on all objects in a scene.

Diffused Light:

Unlike in the case of ambient lighting where a distributed light source is assumed, the intensity profile across the surface changes when exposed to a point light source. This is because light from the source is incident at a different angle at different points of the surface. The model which represents such diffused reflection is based on Lambert’s cosine law and it is given by,

I_diff = I₁k_dcosθ

Specular Reflected Light:

Typical shiny surfaces like polished metal, oily skins, porcelain, etc, that are neither diffuse reflectors nor ideal reflectors like reflecting light specularly when exposed to a point light source. Such reflection is identified by a highlight or bright spot on the surface when viewed from particular directions. Most interestingly such spots appear to move over the surface with the movement of the viewpoint. This is called Specularly Reflected Light.

Distance Factor:

We know that the intensity of light energy falls off as it travels farther from the light source. So, the intensity profile of two identical surfaces, under even lighting conditions, can’t be identical if they are at different distances from the light source and/or viewpoint. A factor is commonly known as a distance factor.

Color Factor:

In the illumination models consider only monochromatic lights and surfaces. To model color light and colored surfaces we can assume there are basic components of incident light intensity, namely I_RED, I_GREEN, and I_BLUE and each of the three coefficient of reflection (k_a, k_d, k_s) as three elements (k_RED, k_GREEN and k_BLUE) vector. This is called as Color Factor. It means for a given surface we can have nine different characteristic reflection coefficients that one-to-one correspond with similar color lights only.

Shading:

We have learned how to calculate the intensity of light reflected from a point in a given lighting and surface condition. Now, we have to use a technique for finding the intensity of a surface as a whole to simulate its appearance under the given lighting condition. This technique is called Shading.

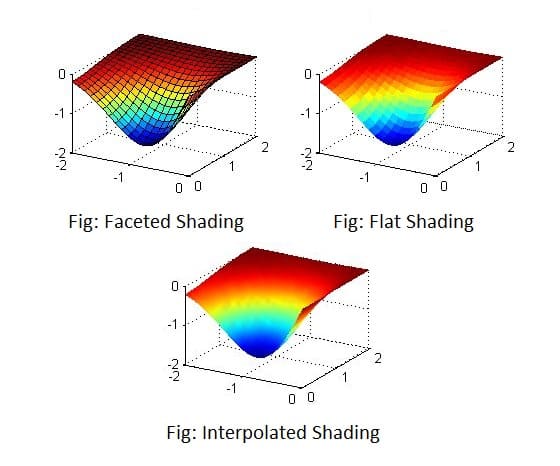
Constant Shading:

It is the simplest shading model for a polygon surface, it is also known as flat shading or faceted shading. Instead of applying the illumination model separately at each point of the surface, this model applies the illumination model only once to determine a single intensity value for a polygon. All points over the surface of a polygon are then displayed with the same intensity value. This approach assumes that:

1. All light sources are at infinity implying N.L and attenuation factor are constant across a polygon surface.
2. The viewpoint is at infinity implying V.R is constant across a polygon surface.
3. The graphic object being modeled as a polygonal face isn’t an approximation to a curved surface.

Interpolated Shading:

Interpolated Shading is a kind of trade-off between computational expense and realistic shading quality. To yield more realistic shading with intensity varying from point to point on a surface needs due consideration to change of curvature, the direction of the incident light, and the position of viewpoint from one point on a surface to another.

Gouraud Shading:

The following steps are required to carry out each polygonal face of the surface mesh for this shading scheme developed by Gouraud.

Step1: Determine the unit normal vector at each vertex of a polygon. If a vertex is shared by some polygon faces the average of the normals to all the faces at that vertex gives the desired normal vector.

Step2: Find the intensities at each vertex by applying illumination models separately using respective vertex normals.

Step3: For each scan line, calculate intensities at the intersection of a scan line with an edge by linear interpolation of intensities at the edge endpoints.

Step4: Calculate intensities at points along a scan line between the edges by linear interpolation of intensities at the intersections of the scan line with the edges.

Phong Shading:

One of the major disadvantages of Gouraud shading is that it avoids finding the surface normal at each point on every scan line. As a result, the change in curvature from point to point is overlooked.

But Phong shading achieves a better approximation to the true shape of a surface and thus a better rendering of the surface by determining surface normals at each point using the linear interpolation technique. Illumination models are applied at every such point using the normal vector calculated at the respective points and quite obviously the process is computationally expensive.