2D Transformation in Computer Graphics Solved Examples

2D Transformation in Computer Graphics:

Translation:

Let us imagine a point P in a 2D plane. Assume that P’s coordinate (x,y) depicts the current position.

Now, if we force P to move Δx distance horizontally and at the same time Δy distance vertically then the changed location of P becomes (x+Δx, y+Δy).

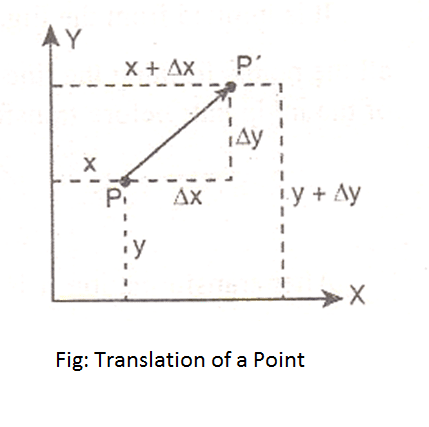
In terms of object transformation, we can say that the original point object p(x,y) translates to becomes P'(x’,y’) and the amount of translation apply is the vector.

Algebraically,
x’=x+Δx
y’=y+Δy

Rotation:

This transformation is used to rotate the objects about any point in a reference frame. Unlike translation, rotation brings about changes in position as well as orientation. The point about which the object rotates, it says the Pivot point or Rotation point.

Rotation about Origin:

Consider a trial case where the pivot point is the origin as shown in the figure:

The rotating point P(x,y) represents as –
x=rcosϕ, y=rsinϕ
where (r, ϕ) is the polar coordinate of P. When this point P is rotated through an angle θ in the anti-clockwise direction, the new point P'(x’,y’) becomes,
x’=rcos(θ+ϕ) y’=rsin(θ+ϕ)

Rotation about an Arbitrary Pivot Point:

The pivot point is an arbitrary point P_p having coordinates (x_p, y_p). After rotating P(x,y) through a positive θ angle its new location is x’y'(P’).

Scalling:

Scaling is a transformation that changes the size or shape of an object. Scaling origin can be carried out by multiplying the coordinate values (x,y) of each vertex of a polygon, each endpoint of a line or the center point and peripheral definition points of closed curves like a circle by scaling factors s_x and s_y respectively to produce the coordinate (x’,y’).
The mathematical expression for pure scaling is: