Cohen-Sutherland Line Clipping Algorithm

Cohen-Sutherland Line Clipping:

It is one of the most popular line-clipping algorithms. The concept of assigning 4-bit region codes to the endpoints of a line and subsequent checking and operation of the endpoint codes to determine totally visible lines and invisible lines (lying completely at one side of the clip window externally). Cohen-Sutherland Line Clipping Algorithm was originally introduced by Danny Cohen and Ivan Sutherland.

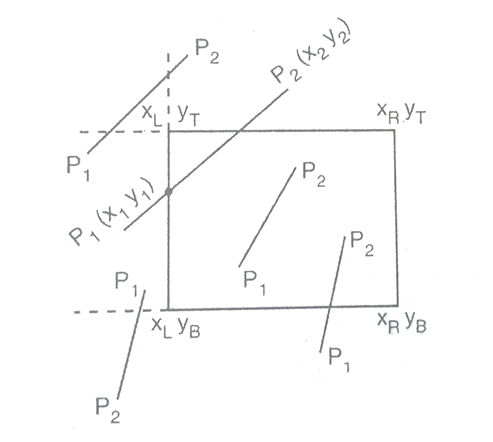
For clipping other invisible lines and partially visible lines, the algorithm breaks the line segments into smaller subsegments by finding intersections with appropriate window edges. For a pair of a non-zero endpoint and an intersection point, the corresponding subsegment is checked for two primary visibility states as done in the earlier steps. The process is repeated till two visible intersections are found or no intersection with any of the four visible window edges is found. Thus this algorithm cleverly reduces the number of intersection calculations.

Steps of Cohen-Sutherland Line Clipping Algorithm:

1. Input: x₁, x_R, y_T, y_B, P₁(x₁, y₁), P₂(x₂, y₂)

Initialize i=1
while i<=2

i=i+1
end while
i=1

2. Intialize j=1

while j<=2

3. if codes of P₁ and P₂ are both equal to zero then draw P₁P₂ (Totally Visible)
4. if logical intersection or AND operation of code – P₁ and code -P₂ is not equal to zero then ignore P₁P₂ (Totally invisible)
5. if code -P₁=0 then swap P₁ and P₂ along with their flags and set i=1
6. if code – P₁< >0 then
for i=1
{
if C_{1 left}=1 then
find interaction (x_L, y’_L) with left edge
assign code to (x_L, y’_L)
P1=(x_L, y’_L)
end if
i=i+1
go to 3
}
for i=2
{
if C_{1 right}=1 then
find interaction (x_R, y’_R) with right edge
assign code to (x_R, y’_R)
P1=(x_R, y’_R)
end if
i=i+1
go to 3
}
for i=3
{
if C_{1 bottom}=1 then
find interaction (x’_B, y_B) with bottom edge
assign code to (x’_B, y_B)
P1=(x’_B, y_B)
end if
i=i+1
go to 3
}
for i=4
{
if C_{1 top}=1 then
find interaction (x’_T, y_T) with top edge
assign code to (x’_T, y_T)
P1=(x’_T, y_T)
end if
i=i+1
go to 3
}
end