Bézier Curve in Computer Graphics
Bézier Curve
Bézier Curve Spline can fit to any number of control points. Without tangent vector specification at any of the control points, a set of characteristics polynomial approximating functions that say Bézier Blending Functions. It blends the control points to produce a Bézier curve segment. However, the degree of a Bézier curve is determined by the number of control points to be fitted with that curve segment.
Given a set of n+1 control points P0, P1,…, Pn a parametric Bezier curve that will fit those points is mathematically defined by,
Now restricting our attention to Bezier curves of degree 3 (n=3). We find that four (n+1) control points are required to specify a cubic Bezier curve segment. Thus for a Parametric cubic Bezier curve,
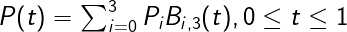
or, P(t)=P0B0,3(t) + P1B1,3(t) + P2B2,3(t) + P3B3,3(t)
Tangent Bézier Curve:
Although it is not necessary to numerically specify the tangent vectors at the end of a Bezier curve, finding out the expression for them will bring out more interesting facts about the Bezier curves. The parametric tangent vector is obtained by differentiating a cubic Bezier curve segment.